Using Computers to Compute: Calculating Sine and Cosine Using CORDIC
I gave this presentation at a Bellingham.Codes meeting on July 26th, 2018:
Using Computers to Compute: Calculating Sine and Cosine using CORDIC
Update
Unfortunately, the animations in the PDF only work in Adobe Acrobat. Evince and Sumatra PDF both show blank slides where there should be an animation of CORDIC calculating it's output. So I'm now including the contents of the presentation as HTML here. I also fixed a few minor math mistakes (but left the slides alone).
Summary
How do computers evaluate mathematical functions? In this talk I describe the CORDIC algorithm for calculating trigonometric functions on simple computers, for example a pocket calculator's microprocessor.
Introduction
Overview
I will talk briefly about the following topics:
- What are sine and cosine?
- How do humans do math?
- How do simple computers do math?
- What is CORDIC?
- How does CORDIC work?
- Including graphic examples
Why?
- It's fun
- Tau Day (6/28). Last month's meeting was a social, so this talk is late
- History of computing
- Math! Who doesn't like learning how to do math calculations?
- Or at least having a computer spare us the work?
Tau Manifesto Plug
- If you haven't read Michael Hartl's Tau Manifesto, you should.
- tauday.com
- Makes understanding trigonometry much easier
Sine and Cosine
Sine and Cosine
- What are they?
- Trigonometry. Supposedly about Triangles.
- It's really about circles.
Sine and Cosine Illustrated
- Unit Circle:
- Circle of radius 1, centered at the origin, (0,0)
- Theta (θ):
- Angle pointing to point on a circle
- Sine:
- Vertical coordinate of point
- Cosine:
- Horizontal coordinate of point
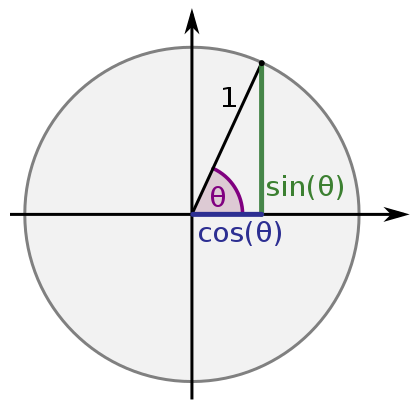
Figure 1: Unit Circle (Credit: Wikipedia)
Why are these functions important?
- Fundamental math
- Used in very many engineering calculations
- Astronomy, Surveying, Navigation, Mechanics, Radio Engineering, Signal Processing
- Converting from rectangular to polar coordinates
- I won't even try to list all the uses
Computing without computers
Computing before digital computers

Tools of the Trade
- Table books (printed spreadsheet)
- Slide rule (fancy lookup table)
- Pencil, paper
- Maybe even a protractor (for minimum accuracy)
- Did you spot the error in the previous slide?
- \(sin \theta\) should have been 0.97029. Oops, I copied the wrong table value.
How are the tables made?
- By hand, with Taylor series like this:
\[sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} +
\frac{x^9}{9!} - \dots \]
\[cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} +
\frac{x^8}{8!} - \dots \]
- That's a lot of multiplications!
- Even after clever optimizations
- We'll get back to that in a minute
- That's a lot of multiplications!
There has to be a better way!


Quick side-note for the unlucky
- If you are stuck working with pencil and paper, this book has you covered.

Calculators
- Okay, so we have calculators.
- But how do they work?
Computer Math
Digital logic for math
- Digital circuits exist to quickly calculate basic arithmetic operations
- Addition, subtraction, bitshift, etc.
- Bitshift is multiplication and division by powers of two only
- Arithmetic Logic Unit (ALU)
Digital logic for math
- Simple computers have no multiplication or division operators
- Why? Multiplication takes multiple steps (more time) and more transistors
- Division takes even more
A simple ALU
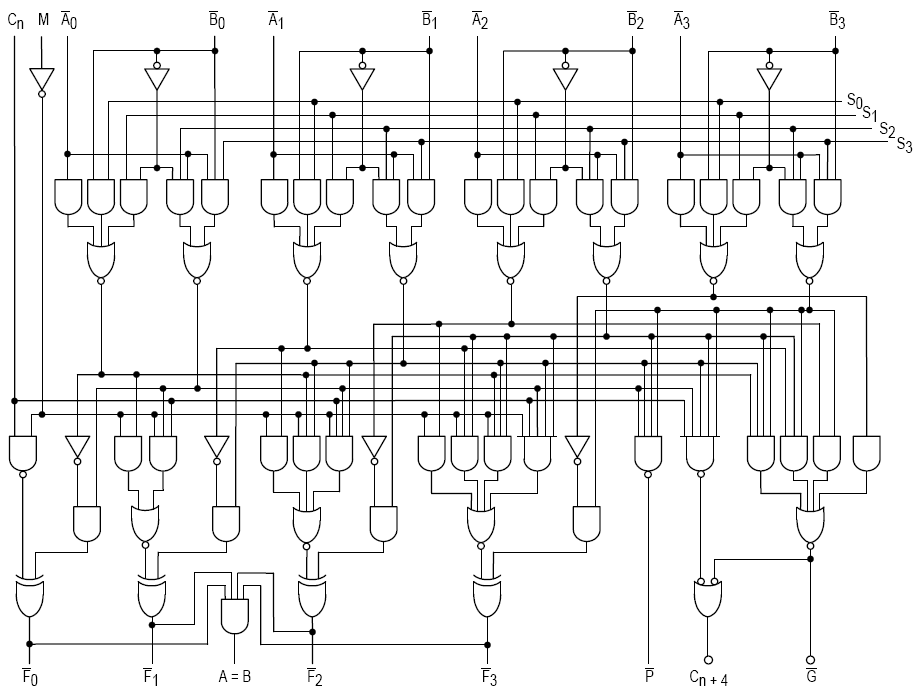
Figure 2: Credit: Wikipedia
- 4-bit ALU schematic, simplified
- Look at this thing
- You don't want to make this even more complicated by building a multiplier too, do you?
CORDIC
Sine and cosine without multiply
- Traditional methods of calculating sine and cosine require slow and expensive multiply circuits
- Can we calculate sine and cosine without multiply circuits?
CORDIC
- COordinate Rotation DIgital Computer
- Jack E. Volder, The CORDIC Trigonometric Computing Technique, IRE Transactions on Electronic Computers, September 1959.

Figure 3: Credit: Journal of VLSI Signal Processing
The CORDIC I Computer
- Special purpose computer to demonstrate algorithm
- 96.5773 kHz clock frequency
- Built in 1960
- Led to CORDIC II built for the Air Force and B-58 bomber
- Replaced analog computers

Figure 4: Credit: Journal of VLSI Signal Processing
The CORDIC benefits
- Uses only:
- Addition
- Subtraction
- Bitshift
- A small table look up
- No multiplications!
- Can be built with the simple ALU circuits
How was it discovered?
- Trigonometric identities:
- Collections of mathematical facts collected over thousands of years
- Not obviously useful at first look, until you see one used well
- This is an example
- "Necessity is the mother of invention." –Jack Volder
An apology
- I'm sorry, but I didn't have time to create images for the following slides.
- We will all have to use our imaginations, or study this part later.
- There are animated examples at the end.
Sneak peek

Quick derivation of CORDIC 1
- Suppose you already know the coordinates of one point on the
circle with angle \(\alpha\)
- \(sin(\alpha)\) and \(cos(\alpha)\)
- What about another point a small angle away?
- \(sin(\alpha+\theta)\) and \(cos(\alpha+\theta)\)
\[ sin(\alpha+\theta) = cos(\alpha) cos(\theta) - sin(\alpha) sin(\theta) \] \[ cos(\alpha+\theta) = sin(\alpha) cos(\theta) + cos(\alpha) sin(\theta) \]
- These equations rotate a known point around the circle
Quick derivation of CORDIC 2
Coordinate Rotation:
\[ sin(\alpha+\theta) = cos(\alpha) cos(\theta) - sin(\alpha) sin(\theta) \] \[ cos(\alpha+\theta) = sin(\alpha) cos(\theta) + cos(\alpha) sin(\theta) \]
Or:
\[ x_{next} = x_{in} cos(\theta) - y_{in} sin(\theta) \] \[ y_{next} = y_{in} cos(\theta) + x_{in} sin(\theta) \]
In code:
x_next = x_in * cos(theta) - y_in * sin(theta) y_next = y_in * cos(theta) + x_in * sin(theta)
Matrix notation
- Graphics programmers might recognize this as an image rotation matrix
\[ P_{next} = \begin{bmatrix} x_{next} \\ y_{next} \end{bmatrix} = A P_{in}^T = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix}\]
Quick derivation of CORDIC 3
Math trick: divide both sides of the equation by \(cos(\theta)\).
\[ \frac{x_{next}}{cos(\theta)} = x_{in} - y_{in} tan(\theta) \] \[ \frac{y_{next}}{cos(\theta)} = y_{in} + x_{in} tan(\theta) \]
In code:
x_next = x_in - y_in * tan(theta) y_next = y_in + x_in * tan(theta)
x_next and y_next grow each time we do this (since \(cos(x)<1\)),
but we can fix that later.
Where does this get us?
- So now we can easily add a fixed angle to any sine/cosine result
and get a new point
- If we know the arctangent of that angle
- We can move to any angle/point by repeatedly adding a small angle (say, one degree) to a starting point, until we have the angle we want
- Or, we can be smart about our increments: start big, and get smaller as we zero in on the answer
Binary search for angles
- Idea: start with a quarter rotation, then an eighth, a sixteenth, etc.
- Binary search!
- Need to be able to rotate both forward and backwards (we can)
- So, when our angle sum is higher than our target angle, rotate clockwise.
Final trick
- Choose the angle of our successive jumps so that \(tan(\theta)\) is always a power of two
\[ \frac{x_{next}}{cos(\theta)} = x_{in} - y_{in} 2^{-i} \] \[ \frac{y_{next}}{cos(\theta)} = y_{in} + x_{in} 2^{-i} \]
In code:
x_next = x_in - (y_in >> i) y_next = y_in + (x_in >> i)
Cleanup
- Our point's distance from the origin grows each iteration
- Start with a point inside the unit circle (K, 0)
- It will end up on the unit circle at the end
- I won't show the math for calculating K, but it isn't complicated
8-bit CORDIC code
/* 8-bit CORDIC algorithm for angles in first quadrant. */ const uint8_t arctan_8[8] = { 32, 19, 10, 5, 3, 1, 1, 0 }; const int8_t K_8 = 78 - 1; int8_point_t do_cordic_8 (uint8_t binangle) { /* Calculate sin, cos using CORDIC */ /* Initialize values */ int8_t x = K_8; int8_t y = 0; int8_t z = binangle; /* Error term */ for (int i = 0; i < 8; i++) { int8_t next_x, next_y, next_z; if (z >= 0) { next_x = x - (y >> i); next_y = y + (x >> i); next_z = z - arctan_8[i]; } else { next_x = x + (y >> i); next_y = y - (x >> i); next_z = z + arctan_8[i]; } x = next_x; y = next_y; z = next_z; } int8_point_t result; result.x = x; result.y = y; return result; }
Examples
- The following examples show the CORDIC algorithm seeking the correct result
- In eight steps it gains eight bits of precision towards the correct answer (0.4% max error)
- Created with Dr. Geo geometry software
- Uses Smalltalk language for scripting geometric figures
One radian

One half radian

Two radians

Zero radians

90 degrees

Conclusion
Any Questions?
- Want to know more?
Bonus images
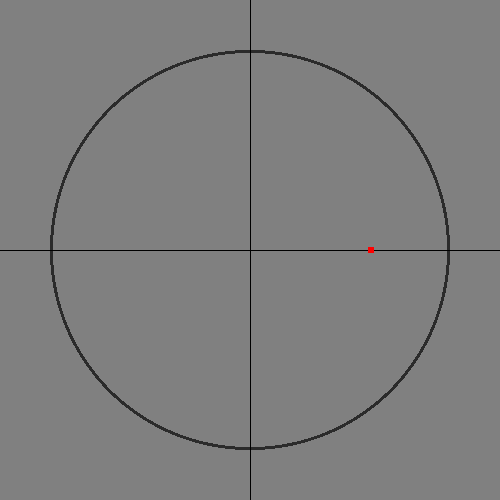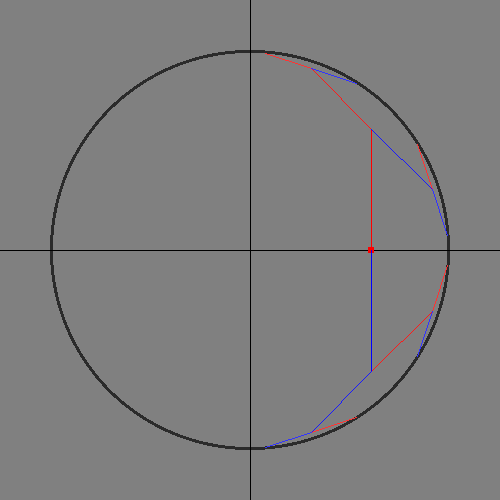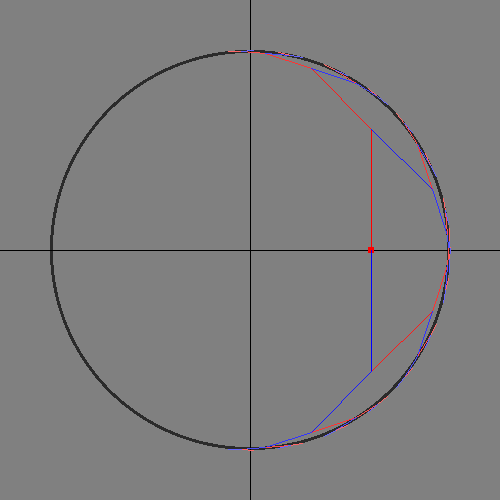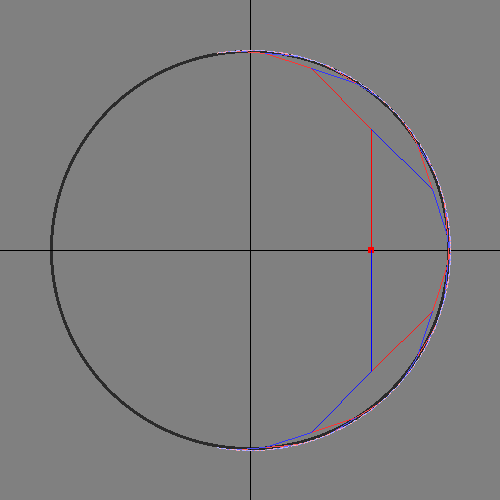
I made these after the original presentation. They show how the domain of the CORDIC calculations covers slightly more than half the unit circle. Input angles outside that domain need to be rotated before and after CORDIC.
Depth-first search space
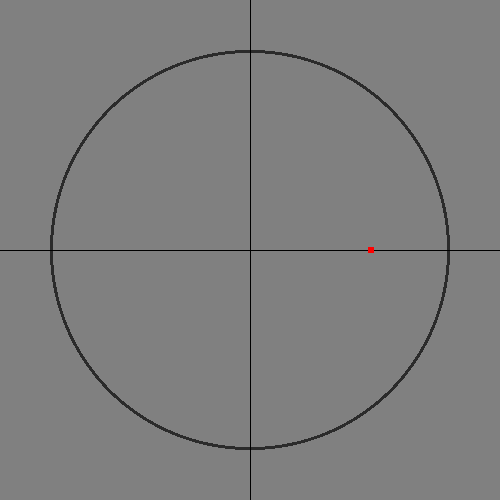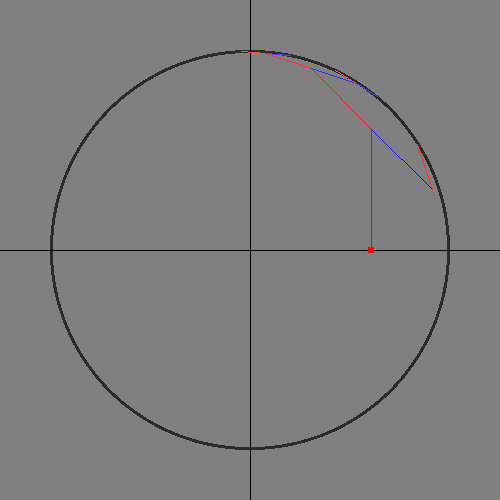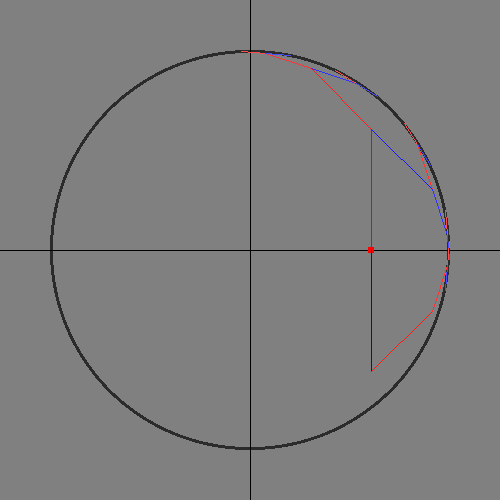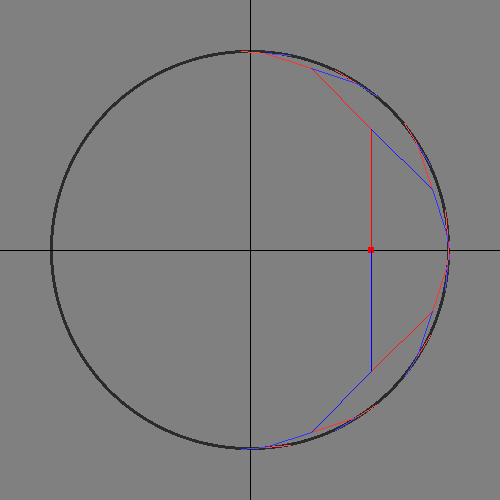
Breadth-first search space